Interactive Distance Formula (Pythagorean theorem)

The distance formula is as follows.
a² + b² = c² Let's change those variable names to make things clear.
Let's say that our horizontal distance is x and that our vertical distance is y.
x² + y² = distance²
distance = sqrt(x² + y²)

Let's start simple

Let's find the distance between (0, 0) and (5, 0), this problem doesn't require the distance formula, although it would work, because it's a non-diagonal line.
There is no change in y between the points; 0 - 0 = 0.

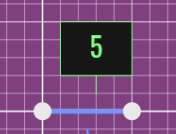
How do we find the distance of a non-diagonal line?
Remember the number line?
We subtract the numbers and if our result is negative we make it positive because a negative distance is impossible.
That's it and that's all.
5 - 0 = 5
or
| 0 - 5 | = 5 Simple enough, when our points form a non-diagonal line, all we need is subtraction.
However, measuring a diagonal line is harder.

Let's find the distance between two diagonal points

We may have noticed that the distance formula is the Pythagorean Theorem which works with triangles, not two points.
What does finding the distance between two points have to do with triangles?
Let's try an example problem.

Let's make it easy on ourselves, let's make two points (4, 3) and (0, 0).

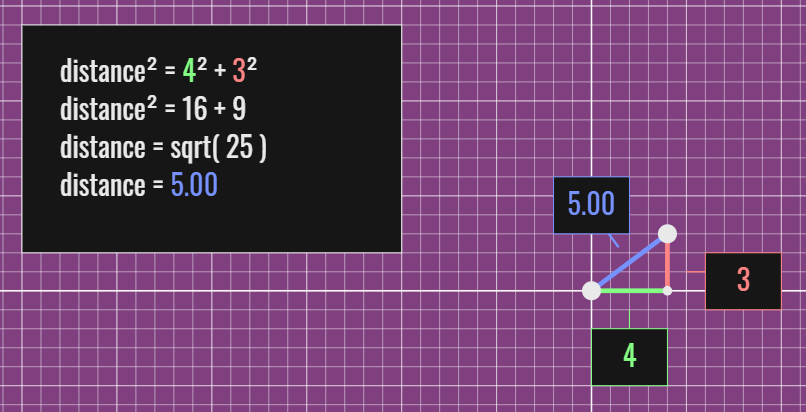
We already know how to measure the distance of non-diagonal lines; Let's turn our diagonal line into two non-diagonal lines.
horizontal distance = x = 4 - 0 = 4
vertical distance = y = 3 - 0 = 3 Good start.
But that is not quite enough.
What to do with our horizontal distance and vertical distance.
What if we add them together?
We intuitively know the distance between the points isn't 7. That's too far.

What if we connect our two non-diagonal lines with a diagonal line?
We've created a right triangle.
We can find our distance by finding the length of our hypotenuse.
How do we do that?
Exactly, we use the distance formula, which is a use of the Pythagorean Theorem.
x² + y² = distance²
(4 - 0)² + (3 - 0)² = 25
16 + 9 = 25 So we take the square root of both sides and we get
sqrt(16 + 9) = 5

Some Intuition

We expect our distance to be more than or equal to our horizontal and vertical distances.
Because the shortest path is a straight line, we expect our distance to be less than or equal to our horizontal and vertical distances added together.

We can see that the distance between two points is related to the angle between the points.

Conclusion

We can find the distance between two points by constructing a triangle, where the legs are the horizontal and vertical distance, and the hypotenuse is the overall distance.
We have known how to find the length of the hypotenuse for millennia, thanks to Pythagoras.