Interactive Fractions (Division)
What Does The Denominator Represent
The denominator is the bottom number of our fraction.
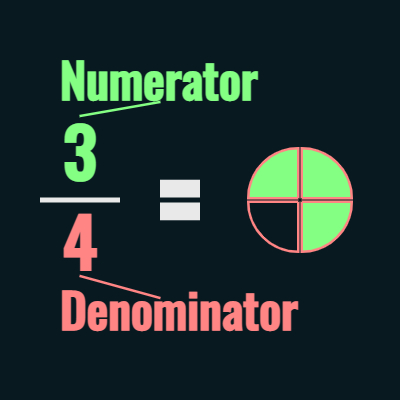Figure A
Normally it's the default unit value of 1, that's because we usually deal with "whole" units.
For example, if we asked someone for 2 bananas, we would expect 2 whole bananas because it's understood that our unit size is 1.
However, if someone is selling frozen chocolate-dipped banana halves (1/2), and we order 2 (units),
we'd expect 2 orders, but 1 banana because the unit size was 1/2 of a banana per order.
2 * (1/2) = 2/2 = 1
Figure B
When our denominator is 1, we don't have to write it because it is assumed,
for example in Figure B we could leave out the denominator and the picture would still be correct.
What happens when we change our denominator?
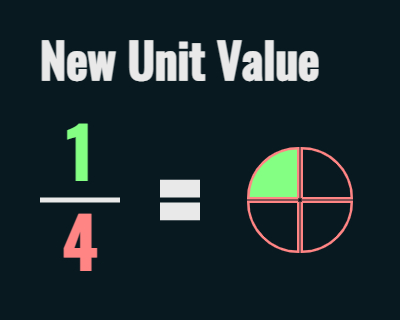Figure C
When we change our denominator, we're changing our unit size.
We see how the unit size changed from a full circle in figure B to a quarter circle in figure C, that's because we changed the denominator.
Let's look at the example of 3/4
Our unit size becomes 1/4 like in figure C.
3/4 = 3 * (1/4)
That is, we have 3 units of (1/4).
Figure D
A Look At Integers
When we don't have a denominator, we can think of our denominator as our default unit size of 1,
3/1 = 3
We can view any interger as a fraction with the denominator of 1.
3 * (1/1) = 3
We also note that any integer divided by 1 gives us that the same integer.
64/1 = 64
We see adding a denominator of 1 doesn't change the value of our integer.
128/1 = 128
1/1 = 1
What Does The Numerator Represent
The numerator is the top number of our fraction (see figure A).
The denominator tells us the value of our unit, the numerator tells us how many units we have.
3/4 = 3/1 * 1/4
Our denominator is 4, so our unit value is 1/4.
or
3/4 = 3 * 1/4
or
3/4 = 1/4 + 1/4 + 1/4
Our numerator is 3, so we have 3 units of (1/4).
The Relationship Between Division and Fractions
Division and a fraction look similar.
In fact, in figure D, are we dividing 3 by 4 or are we showing a 3/4?
Both.
A fraction is a division problem.
We don't always have to execute the division though, sometimes it is convenient to show our number in fraction form.
If we execute the division operation, then we would show the number in decimal form, our example of 3/4 would be 0.75.
Can't Divide By Zero
We can't have a denominator of 0.
Changing our denominator changes our unit size, a unit size of 0 doesn't make sense.
how many zeros do you have?
how many zeros do you want?
how many zeros do you have to add together to get this number?
Those questions don't make any sense, neither does a denominator of 0.
Conclusion
Fractions are fundamental.
When we understand what the numerator and denominator represent, things become clearer.
Resources