Interactive Unit Circle
The unit circle is simple, it's a circle with a radius of 1.
So why is it so useful?
We can see things in their simplest form.
Let's get an intuition of the unit circle by using the interactive below.
Notice that we divide the circle into 4 quadrants (quad means 4), we go counter-clockwise, and the first quadrant is the top-left
Notice the Patterns in Each Quadrant
Memorize the key points in the first quadrant (the top right quadrant).
The other quadrants follow its pattern.
Notice in which quadrants the cosine is negative and in which quadrants the sine is negative.
The number line teaches us that zero separates the positive numbers from the negative numbers, the origin of our unit circle is (0, 0).
All x's to the left of our center are negative.
All x's to the right of our center are positive.
All y's above our center are negative.
All y's below our center are positive.
Learn more about the number line here.
We just need to remember a few key points in the first quadrant and we have most of what we need.
Remember the Pythagorean Theorem
a2 + b2 = c2
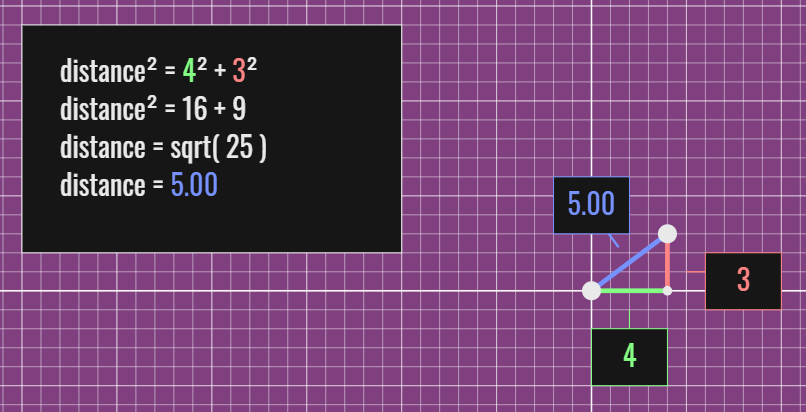Figure A
In the case of the unit circle it looks like the following.
Cosine(angle)2 + Sine(angle)2 = 1
We can test this out above and see that it holds for all angles.
We notice that the cosine is our x coordinate and the sine is our y coordinate.
The Pythagorean Theorem is also called the "distance formula" because it returns the distance between two points.Notice in the unit circle the distance formula of the cosine and sine always returns 1.
This is exactly what we expect since the radius of the unit circle is 1. (cosine(angle), sine(angle)) is one point, what is the second point? (0, 0) We can learn more about the distance-formula (Pythagorean Theorem) here
Sine, Cosine, and Tangent - SOH CAH TOA
Sine = Opposite/Hypotenuse
Cosine = Adjacent/Hypotenuse
Tangent = Opposite/Adjacent
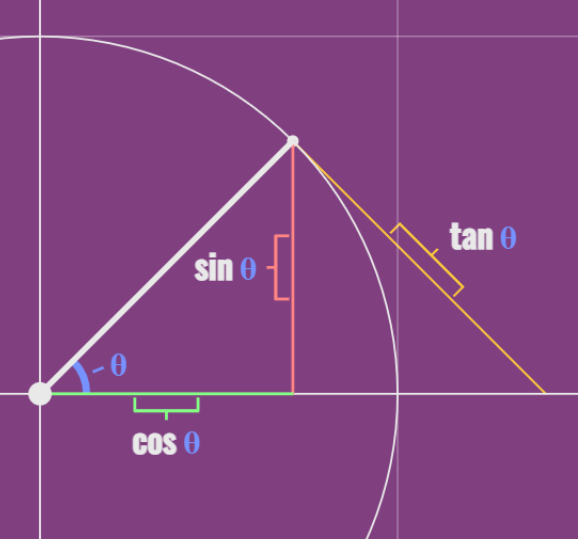Figure B
We know that the Hypotenuse is 1, therefore the Sine is Opposite/1.
Because dividing any number by 1 returns the number, we can see that we can skip the division by 1 step.
Therefore, in the unit circle, the Sine is the Opposite side.
The same logic applies to the Cosine, it is simply the Adjacent side.
Simplicity is part of the unit circles' beauty.
What Does Tan Represent
We have our x from the cosine function and our y from the sine function.
So what does the tan function return?
Well if we already have our x and y.
Then we draw a circle from (0, 0) to our x and y.
Then we draw a line from our x and y to the x-axis where the line only touches our circle once.
The length of that line is what the tan function represents, for example the orange line in Figure B.
All Points Can Be Expressed with the Unit Circle
We can view all points as being scaled from some point on the unit circle.
An easy way to think about this is in one dimension, any number can be expressed from a unit number, namely 1.
For example, 64 is simply 1 counted 64 times, 128 is 1 counted 128 times, and .5 is one halved.
This is a similar idea to what we explore when in our article on linear transformations.
Conclusion
The unit circle is a tool to help us, not to burden us.
A basic understanding of how the unit circle works is superior to memorizing a few points.
A good understanding of the unit circle will bear fruit throughout our mathematic careers.
Resources